Ratio M2: una elegante forma de expresar el binomio rentabilidad / riesgo
Franco Modigliani (1918-2003) es conocido como uno de los mejores economistas del S-XX (Nobel en 1985). Entre sus aportaciones más destacadas se pueden citar el teorema de Modigliani-Miller, sobre la estructura de financiación de una empresa, o la hipótesis del Ciclo de vida, sobre los patrones de consumo y ahorro. Pero a Modigliani le pasa como a Keynes: son menos conocidas sus aportaciones en el terreno de la gestión de carteras. En 1997 propuso, junto a su nieta Leah Modigliani, el ratio M21.
Este ratio mide la rentabilidad que habría tenido una cartera si hubiera tenido la volatilidad de otra (normalmente, la de su categoría). Es decir, homogeneiza las diferencias en el nivel de riesgo para poder comparar las rentabilidades. Así, cuanto mayor es el índice de Modigliani, mejor ha sido la gestión de la cartera.
El índice se obtiene sustituyendo en la función de rentabilidad / riesgo de la cartera su desviación típica por la de la categoría. Para el cálculo se supone que aquellos fondos que han tenido un riesgo inferior al del mercado de referencia toman prestado al tipo del activo libre de riesgo hasta alcanzar el mismo nivel de riesgo que el mercado. Por su parte, se supone que las carteras que han tenido un riesgo superior invierten en el activo libre de riesgo en la cantidad necesaria para tener un nivel de riesgo igual que la del total del mercado (o el del benchmark). De este modo, estamos suponiendo que existe una relación lineal entre la rentabilidad y el riesgo de los fondos. La fórmula se recoge en la siguiente ecuación.
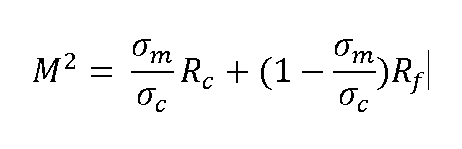
Siendo Rc la rentabilidad de la cartera, Rf la rentabilidad del activo libre de riesgo, sC la volatilidad de la cartera y sm la volatilidad del mercado.
Veamos un ejemplo.
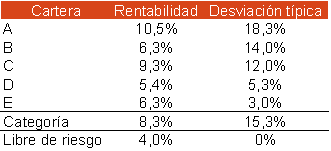
Aplicando la ecuación, los resultados son los siguientes:
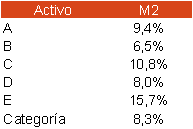
El índice M2 nos indica la rentabilidad que obtendría cada cartera si tuviera una desviación típica de 15,3%, es decir, la que corresponde a su categoría (el M2 de la categoría coincide con su rentabilidad: 8,3%).
De esta forma, podemos concluir que en términos de M2, la cartera E es la mayor calidad, ya que es la remunera el riesgo asumido de forma más que proporcional. Estos resultados están en línea con lo que nos indica el ratio de Sharpe, demostrándose la relación positiva entre ellos dos.
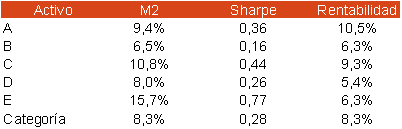
De forma gráfica, se puede comprobar que la función rentabilidad / riesgo de la cartera E tiene más pendiente que la del resto, es decir, tiene un mayor Sharpe. El resultado de cada cartera está representado por un círculo en el gráfico 1.
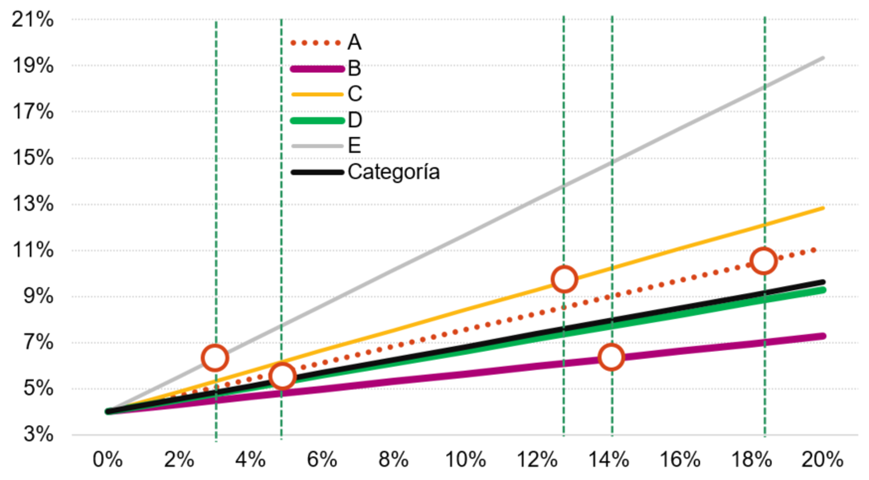
¿Qué hace el ratio M2? Desplazar todos los círculos a lo largo de su función rentabilidad/riesgo hasta la vertical del benchmark (gráfico 2), lo que permite su comparación (en este caso, visual). La cartera más rentable (la A, con un 10,5%) no es la que presenta la mejor proporción con el riesgo asumido (su Sharpe no es elevado). En términos de rentabilidad/riesgo, la mejor cartera es la E (su M2 es el mayor, del 15,7%).
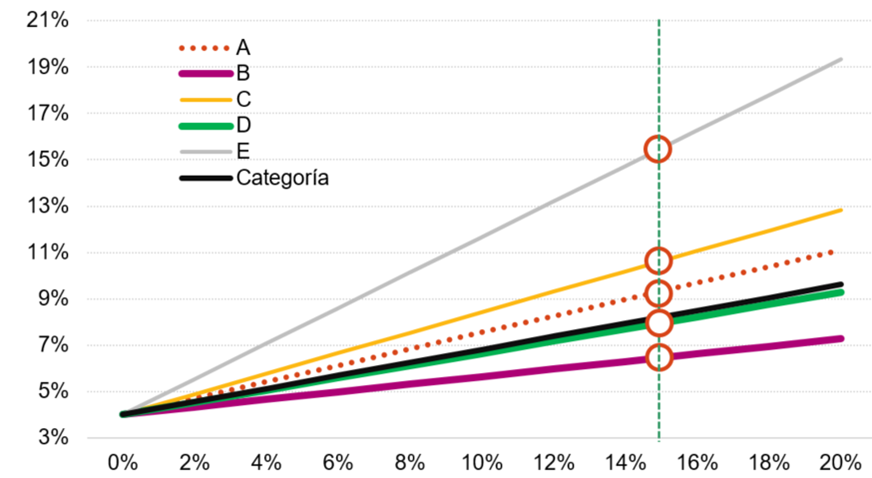
En conclusión, el M2 es una forma elegante de expresar la rentabilidad / riesgo que permite comprobar de forma directa que cartera muestra un mejor binomio.