Tipo de interés implícito. Cálculo e interpretación
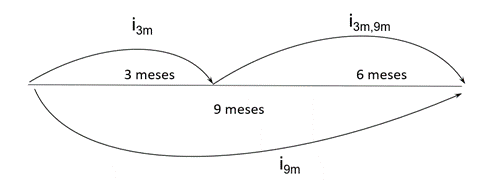
Existen dos acepciones de “tipo de interés implícito”. Por un lado, la rentabilidad que se obtiene invirtiendo en un activo sin flujos de caja, como diferencia entre el capital final y el importe pagado. De ello ya hablamos en este post. El concepto tipo de interés implícito también se utiliza para designar aquel tipo a futuro que hace coherentes los niveles actuales de la curva de tipos de interés. Así, por ejemplo, para un tipo de interés actual a 3 meses (i3m) y otro a 9 meses (i9m) se puede calcular un tipo de interés a 6 meses dentro de 3 meses (i3m,9m) que los hace compatibles (gráfico 1).
Gráfico 1. Tipos de interés a 3m y a 9m y tipo de interés implícito a 6 meses dentro de 3 meses
Porque hoy debe ser equivalente invertir a 3 meses y posteriormente a 6 meses a hacerlo directamente a 9 meses. Para un capital Q, la primera alternativa (invertir a 3m y después a 6m) genera un capital final de:
Q x (1 + i3m x 3/12) x (1 + i3m,9m x 6/12)
Esto es así porque suponemos que el capital obtenido al cabo de los 3 primeros meses (Q x (1 + i3m x 3/12)) lo invertimos durante los siguientes 6 meses al tipo i3m,9m. Pues bien, este capital final debe ser igual que el que se obtenga invirtiendo Q durante 9 meses a i9m:
Despejando:
i3m,9m =


Y lo que sabemos es que, para que la estructura de tipos sea coherente, ambas cantidades deben coincidir.
Despejando:
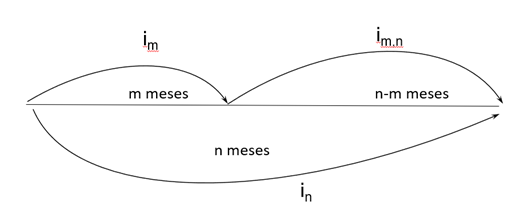
Y, de forma genérica, podemos decir que el tipo de interés al plazo n-m esperado dentro de m meses (im,n) se calcula según la ecuación 1.
Ecuación 1. Tipo de interés implícito (plazo inferior a 12 meses)
Gráfico 2. Tipos de interés a m y a n meses y tipo de interés implícito a n – m meses dentro de m meses

 Por ejemplo, si el tipo de interés a 3 meses es el 3,28% y el tipo a 9 meses es el 3,5%, ¿qué tipo de interés implícito a 6 meses dentro de 3 meses hace coherentes estos tipos?
Por ejemplo, si el tipo de interés a 3 meses es el 3,28% y el tipo a 9 meses es el 3,5%, ¿qué tipo de interés implícito a 6 meses dentro de 3 meses hace coherentes estos tipos?Aplicando la ecuación 1 (m es 3 meses y n es 9 meses):
comprobamos que el resultado es 3,588%
De este modo, i3,9 = 3,588% es el tipo de interés que hace indiferente ambas alternativas de inversión. Es decir, obtendremos el mismo rendimiento invirtiendo el capital a 9 meses al 3,5% que invirtiendo durante los 3 primeros meses al 3,28% y los 6 meses restantes al 3,58%. Esta es una interpretación, por lo tanto, matemática: el tipo de interés implícito es aquel que hace coherente la curva de tipos.
Pasemos a una interpretación algo más financiera. Podríamos decir que el tipo de interés implícito es aquel sobre el que debemos tener una previsión para decidir si invertir a 3 meses y luego a 6 meses o hacerlo directamente a 9 meses. De esta forma, si crees que el tipo a 6 meses dentro de 3 meses va a ser más alto que el 3,588% (es decir, superior al implícito), entonces invertirás a 3 meses al 3,28%, esperando poder reinvertir dentro de esos 3 meses a un tipo superior al 3,588%, obteniendo un mayor rendimiento que si hubieras invertido a 9 meses al 3,5%. Y si, en sentido contrario, piensas que dentro de 3 meses el tipo a 6 meses estará por debajo del tipo implícito, entonces optarás por invertir a 9 meses. Es más, incluso te plantearás endeudarte a 3 meses para renovar al vencimiento la financiación a 6 meses, esperando hacerlo a un tipo menor al 3,588%, obteniendo así una plusvalía. Como es obvio, si crees que el tipo a 6 meses dentro de 3 meses va a estar por encima del implícito, podrás obtener rendimiento positivo endeudándote a 9 meses y, de forma automática, invertir a 3 meses, confiando en que dentro de este plazo podrás invertirlo a 6 meses a un tipo mayor que el implícito. Como se observa, ya hemos incorporado nuestras expectativas, que las compararemos con el tipo implícito y, si hay diferencia, optaremos por invertir y, de forma adicional, por pedir prestado. Y eso hacen todos los miembros del mercado, por lo que podemos decir que el tipo de interés implícito es un estimador de las expectativas del mercado (1).
Supongamos que el conjunto del mercado cree que el tipo de interés a 6 meses dentro de tres meses se situará en el 3,75% (y no en el 3,588%). Entonces, pedirán prestado a 9 meses al 3,5% e invertirán a 3 meses al 3,28%. Ante la mayor demanda de financiación a 9 meses, los que ofrecen esos fondos subirán el tipo de interés. ¿Hasta qué nivel? Hasta aquel en el que la demanda desaparece. ¿Cuál será según nuestro ejemplo?
Recuerda que:
Ahora la incógnita es i9m dado que i3m sigue siendo 3,28% y ahora sabemos que i3m,9m es 3,75%:
i9m = ((1 + 3,28% x 3/12) x (1 + 3,75% x 6/12) – 1) x 12/9 = 3,614%
Es decir, el tipo de interés a 9 meses pasará del 3,5% al 3,614%. ¿El motivo? El cambio de las expectativas del mercado. Ahora, el tipo de interés implícito a 6 meses dentro de 3 meses no es el 3,58% sino el 3,75%. El mercado espera más subida de tipos, y de ahí que la curva tenga ahora más pendiente (diferencia entre el tipo de interés a un plazo mayor menos el tipo a un plazo menor). Cuanto más suba el tipo implícito, más subirá el tipo a 9 meses y, con ello, la pendiente.
¿Y qué pasa si el conjunto del mercado considera ahora que los tipos van a bajar? Es decir, que el tipo a 6 meses dentro de 3 meses va a ser el 3,0%? Ese cambio lo veremos reflejado en el tipo a 9 meses, que cederá hasta el 3,11%. Así es: ahora la curva tiene pendiente negativa, como consecuencia de las expectativas del mercado para una rebaja de tipos de interés en el futuro.
i9m = ((1 + 3,28% x 3/12) x (1 + 3,00% x 6/12) – 1) x 12/9 = 3,110%
En definitiva, observamos que detrás de todo tipo de interés hay una expectativa del mercado y que los cambios de éstas son los que, precisamente, provocan los movimientos de las curvas de tipos de interés. Cuanto mayor sea la cuantía de la subida descontada, mayor será la pendiente positiva de la curva. Cuanto mayor sea el recorte de tipos esperado, mayor será la pendiente negativa. Ahora bien, que el tipo de interés implícito sea un estimador de las expectativas del mercado no implica que sea un estimador del tipo de interés que se dará en el futuro. De hecho, el mercado falla, y mucho, a la hora de anticipar la evolución de los tipos de interés. Pero eso lo dejamos para otro post.
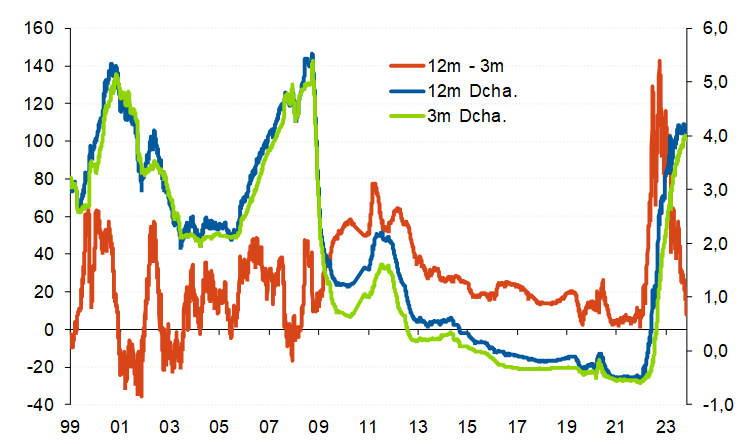
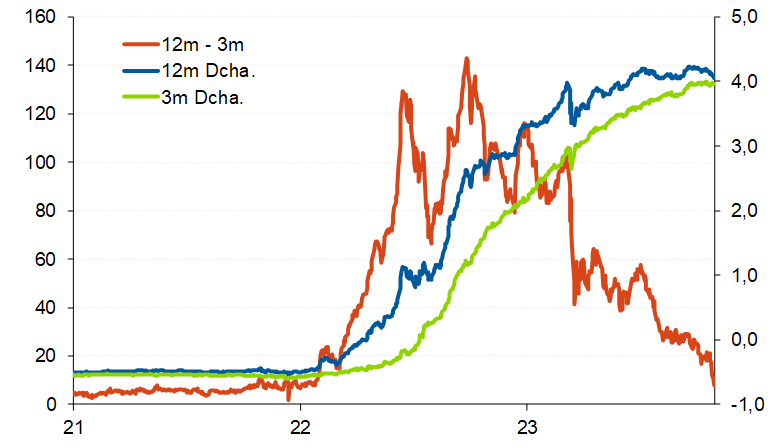
Evolución del Euribor 12m y 3 m y de la pendiente