La TIR como estimador de la rentabilidad en renta fija

Como es sabido, el precio de un bono puede diferir a su valor nominal, lo que provoca que la rentabilidad de la inversión (TIR) pueda ser distinta de la que se consigue vía cupón. Se pueden definir tres casos generales:

• a) Si se paga por el bono un precio inferior al nominal, la TIR será superior al cupón¹.
• b) Si se paga un precio superior al del nominal, la TIR será inferior a la del cupón.
• c) Si se paga el precio igual al nominal, la TIR obtenida coincidirá con el cupón.
   

De esta forma, la TIR (que no el cupón) es el mejor estimador de la rentabilidad que se va a obtener invirtiendo a vencimiento en un instrumento de renta fija. Sin embargo, la TIR no es un estimador perfecto, ya que la rentabilidad dependerá del tipo al que se reinviertan los cupones recibidos. Sólo en un instrumento de cupón cero la TIR es un estimador perfecto de la rentabilidad a vencimiento.

En este post queremos analizar si la TIR es un buen estimador de la rentabilidad que obtenemos al invertir a un plazo inferior al vencimiento del bono. Por ejemplo, si la TIR a la que adquirimos un bono a 10 años es un buen estimador de la rentabilidad que vamos a obtener en el plazo de 3 meses. Para hacer este análisis, tomamos el índice Afi de Deuda Pública española a 10 años y realizamos desde el 1 de enero de 1996 inversiones con un horizonte temporal de 3 meses. Así vamos a comparar la rentabilidad obtenida al final de cada trimestre con la TIR de compra (en total, contamos con 96 observaciones).

TIR a la compra (eje X) y rentabilidad de la inversión a los 3 meses.

Índice Afi de Deuda Púbica a 10 años.

Fuente: Elaboración propia.
 

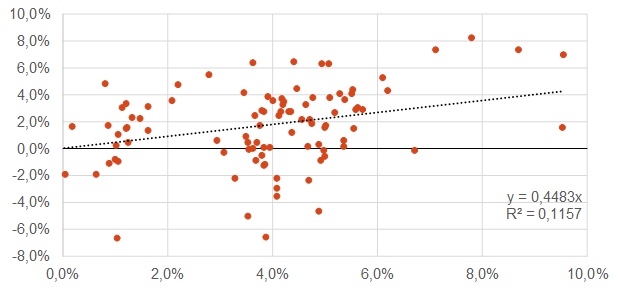
Según se observa en el gráfico 1, la capacidad explicativa de la TIR es muy reducida: apenas un 11,57% (R² de la regresión). Es decir, otras variables tienen mayor poder explicativo de la rentabilidad cuando el horizonte de inversión es inferior al vencimiento del bono (en especial, como se verá en futuros post, cuanto mayor sea la diferencia entre el horizonte de inversión y la duración del bono).

Añadimos un parámetro adicional en la regresión: el producto de la duración y la variación de TIR.

 

 

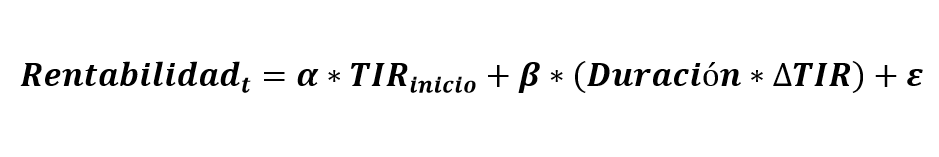
Ahora los resultados son los siguientes:

 

 

Es decir, la rentabilidad que obtenemos en el horizonte temporal no sólo depende de la TIR inicial, sino también de la variación de la TIR multiplicada por la duración del bono. Si introducimos esta segunda variable, la capacidad explicativa se eleva hasta el 0,975 (R²). Aun así, la explicación no es completa ya que habría que tener en cuenta otros factores como el ¿ajuste por convexidad¿, pero que, debido a su menor importancia cuantitativa, lo obviamos en este post.

Podemos concluir que, en el caso del bono a 10 años, en horizontes temporales a 3 meses, la TIR inicial solo explica parcialmente la rentabilidad, siendo más importante la variación de la TIR. Esta variación de los tipos de interés (el ¿movimiento de la curva de tipos¿) y su impacto en el precio del bono vía duración es el denominado riesgo de mercado que, para casos con bonos con elevada duración, es muy importante.

Función de distribución de los rendimientos (eje X) trimestrales.

Índice Afi de Deuda Púbica a 10 años.

Fuente: Elaboración propia.
 

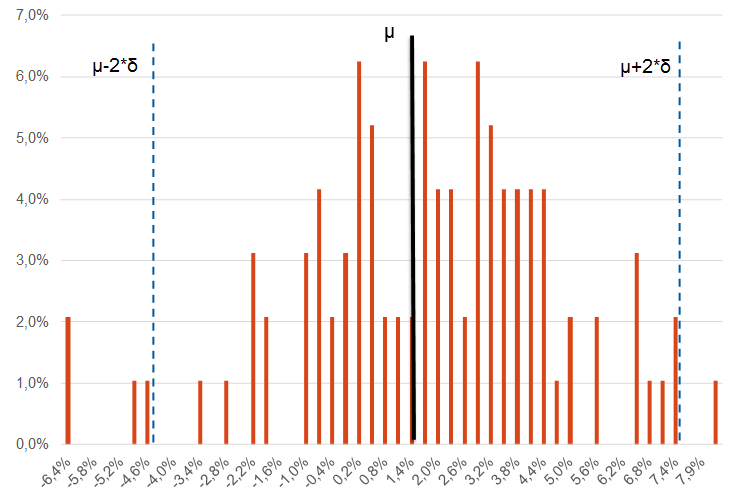
Esto se ha puesto de manifiesto en la mejora de la recta de regresión. Otra forma de verlo es mediante la función de distribución de las rentabilidades trimestrales (gráfico 2). Su media es del 1,68% pero, y he aquí lo más importante, su volatilidad (desviación típica) es del 2,92%. Así pues, el rango de rentabilidad en un trimestre invirtiendo en un bono a 10 años, con un 95% queda definido entre -5% y +7% (aproximadamente). Un rango muy amplio o, desde luego, mucho más de lo que suele pensar un inversor no ¿acostumbrado¿ a la renta fija. En términos anualizados, la volatilidad es del 5,84% (es decir, en un año, la rentabilidad que se obtiene invirtiendo en un bono a 10 años puede oscilar, de forma aproximada entre el -10% y el +10%), lo que pone de manifiesto, de nuevo, que la TIR inicial no es un buen estimador de la rentabilidad que se va a obtener, en especial en bonos con elevada duración y en horizontes temporales cortos.

A partir de aquí, son obvios los dos siguientes pasos en el análisis: modificar los horizontes temporales (6 meses, 12 meses, 3 años y 5 años, por ejemplo) y realizarlo para otros vencimientos. Para próximos post.