Rendimiento implícito vs rendimiento explícito

Cuando se invierte en un activo financiero se está expuesto a dos fuentes de rentabilidad. La primera, denominada “rendimiento explícito”, se deriva del cobro de flujos de caja (cupones, dividendos, etc.) durante el período de inversión. La segunda, denominada “rendimiento implícito” , se produce por la diferencia entre el precio de venta, reembolso o amortización y el precio de compra.

Lo habitual es que los activos ofrezcan las dos fuentes de rentabilidad, es decir, paguen flujos de caja intermedios y, además, se tengan expectativas de cobrar al vencimiento o en la venta un importe mayor al que se pagó. Lo más frecuente es, por lo tanto, que los activos sean de rendimiento explícito.

Pero se pueden encontrar activos que no pagan flujos de caja intermedios. Son los “activos cupón cero”, también conocidos como “activos con rendimiento implícito”. Dado que no hay cobros intermedios, la única forma de obtener un rendimiento es pagando menos de lo que se recibirá. Y dado un precio, la rentabilidad que se consiga dependerá del plazo de la inversión (será mayor cuanto menor sea el precio). Si el plazo es inferior a un año, la rentabilidad se calcula según la ecuación 1 (suponemos que se invierte hasta el vencimiento, momento en el que cobraremos el nominal y de ahí que incluyamos “Nominal” en la fórmula; en el caso de que se venda el activo, o que al vencimiento el importe a cobrar sea diferente al nominal, debe incorporarse en la ecuación esa cifra o el importe de la venta).

Ejemplo: Si pagamos 98 um por un activo que, dentro de 6 meses, en el vencimiento (o en el momento de la venta) devolverá 100 um (u obtendremos ese importe al desprendernos de él), la rentabilidad que obtenemos es del 4,082%. 

Si el plazo de inversión es superior al año, la rentabilidad se calcula según la ecuación 2.

Ejemplo: Si pagamos 97 um por un activo que, dentro de 2 años, cuando venza, devolverá 100 um, la rentabilidad que obtendremos es del 1,53%.

Como es obvio, cuanto menos se pague y menor sea el plazo hasta el cobro final, mayor rentabilidad se obtendrá, como se puede comprobar en la tabla 1.

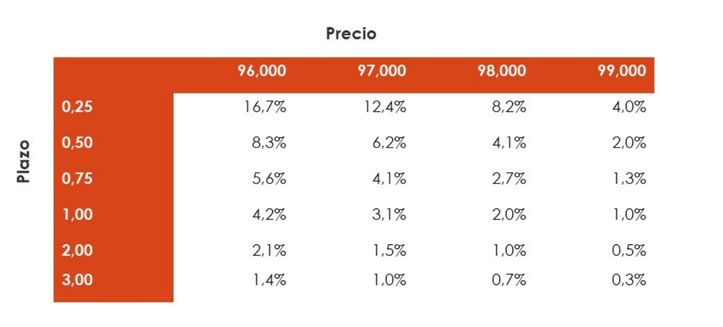
En este punto, surge la siguiente pregunta: ¿cómo es posible que un activo cupón cero genere una rentabilidad negativa? Respuesta: si el precio pagado supera el importe a recibir a vencimiento o en la venta. Supongamos una Letra del Tesoro, un pagaré o un bono cupón cero que dentro de 6 meses (o 2 años), abonará 100 um. Lo razonable es pagar en el momento de la inversión menos de las 100 um. Pero ¿qué sucede si pagamos 102 um? Aplicando la ecuación 1 y 2, respectivamente, comprobamos que la rentabilidad es menor que 0% (tabla 2), en concreto, -3,9% (en el caso del vencimiento a 6 meses) y -1,0% (en el caso del vencimiento a 2 años).

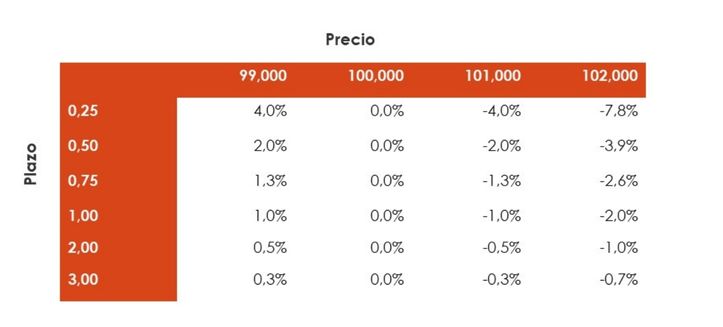
Por lo tanto, si por un instrumento con rendimiento implícito pagamos un precio superior al nominal (o al precio de venta) obtendremos una rentabilidad negativa.

¿Y qué pasa con un activo con rendimiento explícito? Aquí se deben tener en cuenta los flujos de caja que vamos a cobrar. Así, puede suceder que, aunque paguemos más que el nominal o el precio de venta (por ejemplo, desembolsamos 103 um cuando vamos a cobrar 100 um al vencimiento) nuestra rentabilidad sea positiva dado que vía flujos de caja intermedios vamos a recuperar la “pérdida vía capital”.

Veámoslo con unos ejemplos. Supongamos que un activo financiero paga flujos de caja de 5 um y que, a vencimiento, dentro de 3 años, devuelve 100 um. ¿Qué rentabilidad obtendremos si pagamos 100 um? Respuesta obvia: 5%; ¿Y si pagamos menos de 100 um? Pues obtendremos una rentabilidad superior (mayor cuanto menor sea el precio que pagamos). ¿Y si pagamos más de 100 um? La rentabilidad será inferior al 5% ¿Y pude ser negativa? Si, si el importe que pagamos es mayor que el importe de los flujos de caja que vamos a cobrar. Así, si pagamos más de 115 um, entonces obtendremos una rentabilidad negativa. En la tabla 3 se recogen ejemplos para su mejor comprensión (en este caso se trata de un activo con rendimiento explícito y vencimiento 4 años). Si pagamos 100 um, la rentabilidad es igual que el cupón. Si pagamos menos, la TIR es superior al cupón. Y si el desembolso es mayor que el nominal, entonces la rentabilidad es menor que el cupón, siendo negativa si supera el importe de los flujos de caja a cobrar (110 um en el caso del cupón 2,5%; 112 um en el caso del cupón del 3,0% y 114 um en el del 3,5%).

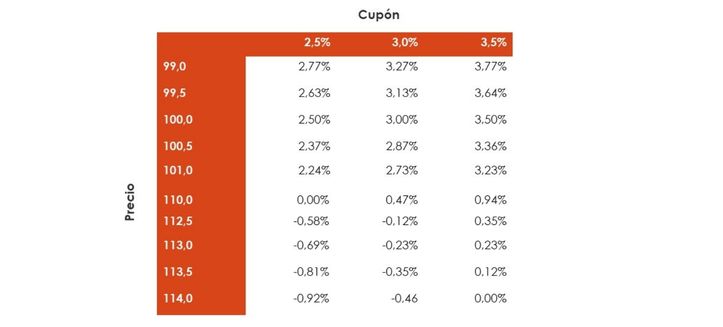
En este caso, “no existe” una fórmula para calcular la rentabilidad, sino que se obtiene a través de un proceso iterativo de aproximación a partir del precio de un bono (ecuación 3).