Beta: medida del riesgo sistemático
La beta o riesgo relativo frente al índice de referencia mide la sensibilidad de la rentabilidad de un título, fondo o cartera de activos a la rentabilidad de su índice de referencia o benchmark. Puede considerarse como un indicador del riesgo sistemático, es decir, del riesgo vinculado al conjunto del mercado. De esta forma, conocer la beta sirve para saber la respuesta de la rentabilidad de un activo frente a la de su índice de referencia, es decir, para tener conocimiento sobre su mayor o menor exposición a los riesgos sistemáticos del mercado en el que se invierte.
Una beta alta implica un mayor riesgo y, por lo tanto, debería estar vinculado a una mayor rentabilidad. Por el contrario, las carteras, fondos o acciones con betas bajas implican riesgos y rentabilidades esperadas inferiores.
Asumiendo el modelo de mercado (CAPM), la rentabilidad de cualquier activo financiero se puede explicar por medio de la regresión expresada en la siguiente ecuación.
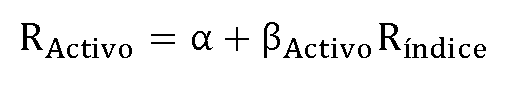
donde:
- RActivo mide la rentabilidad del activo que estamos analizando
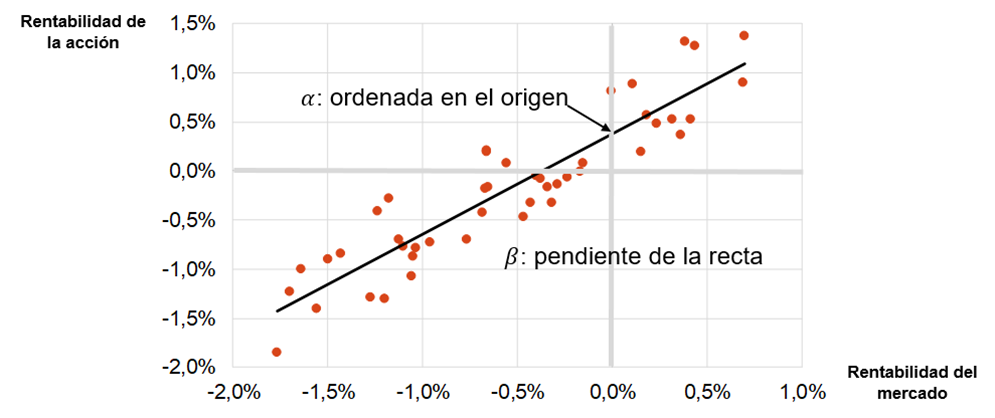
- a es la constante de la recta de regresión, es decir, el corte de la línea con el eje de ordenadas, por lo que se puede interpretar como la rentabilidad de la cartera, fondo o acción ante variaciones nulas del mercado.
- ßActivo es la pendiente de esta recta de regresión, denominada ¿línea característica del título¿, por lo que mide la sensibilidad de la rentabilidad de una cartera respecto a las variaciones de rentabilidad de su índice o mercado de referencia.
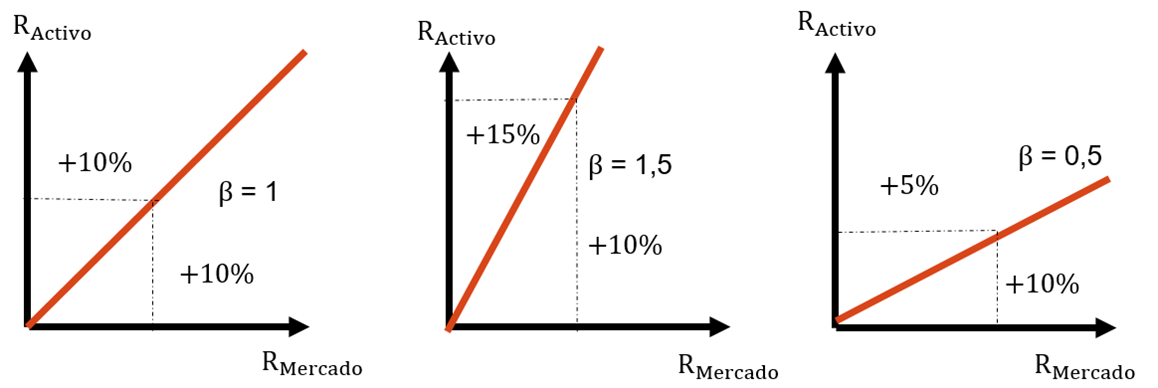
A partir de aquí, se puede distinguir tres tipos de líneas características en función del mayor o menor riesgo, esto es, en función de la beta:
Títulos neutros (ß = 1): El título tiende a fluctuar igual que el mercado.
Títulos agresivos (ß > 1): El título tiende a fluctuar más que el mercado.
Títulos defensivos (ß < 1): El título tiende a fluctuar menos que el mercado.
Es importante señalar que el grado en el que la beta puede explicar el comportamiento de un título o de un fondo depende del poder explicativo de la regresión de la cual proviene. Es decir, hay que tener en cuenta la R2. Así, si la R2 es reducida (por debajo de 0,7), entonces el resultado de la beta no es significativo, no se puede tener en consideración. Porque una cosa es correlación y otra es beta. La beta sólo se interpreta una vez que sé que las dos variables tienen alta correlación. Puede pasar que dos series con una altísima correlación (0,99) tengan beta 0,5, 1, o 1,5. La correlación mide la bondad del ajuste, pero no el grado de sensibilidad de una de las variables respecto a cambios en la otra.
Por último, señalar que otra forma de calcular la beta es dividiendo la covarianza de los rendimientos del activo y del mercado entre la varianza de los rendimientos del mercado.
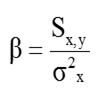
Y dado que sabemos que la correlación es el cociente de la covarianza entre el producto de las desviaciones típicas, otra vía para calcular la beta es mediante el producto de la correlación por el cociente de desviaciones típicas.

Un último comentario. Para calcular la beta (al igual que la covarianza, la correlación, etc.) no se debe hacer con los precios o cotizaciones de los activos o de sus índices de referencia, sino con las tasas de variación.
Ejemplo. Calcular la beta entre la acción ABC y su mercado de referencia a partir de los siguientes rendimientos.
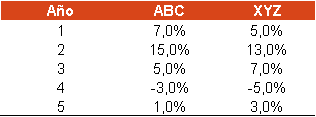
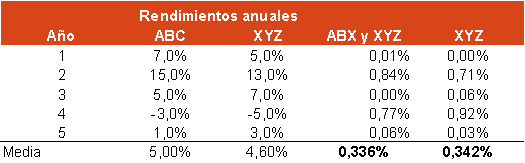
Para calcular la beta necesitamos hallar, por un lado, la covarianza de los rendimientos de la acción y de su mercado y, por el otro, la varianza de los rendimientos del mercado. Para ello, calculamos los rendimientos medios de la acción (5,00%) y del mercado (4,60%). A partir de aquí, restamos a cada rendimiento anual su media y multiplicamos cada resultado, sumándolos todos ellos y dividendo entre el número de datos. De esta forma, obtenemos la covarianza: 0,3360%. Para calcular la varianza del mercado restamos cada rendimiento anual menos su media, elevamos al cuadrado, sumamos todos los resultados y dividimos entre el número de datos. La varianza del mercado es 0,3424%. Dividimos covarianza (0,3360%) entre varianza (0,3424%) y obtenemos la beta: 0,9813.
Otra forma de calcular la beta es obteniendo la línea característica del título, ya que coincide con su pendiente (0,9813).
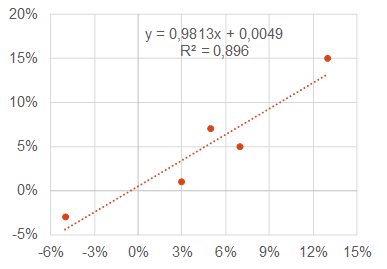
Por otro lado, sabemos que el coeficiente de correlación se calcula como el cociente de la covarianza entre el producto de desviaciones típicas. Éstas son 5,851% (mercado) y 6,066% (fondo), por lo que el coeficiente de correlación es 0,947. Y, por lo tanto, la R2 es 0,8960 (este resultado aparece en el gráfico). Como la R2 es alta, entonces ¿me fío¿ del resultado de la beta, es decir, puede interpretarlo. Como ya hemos comentado, una cosa es correlación y otra es beta. La beta sólo se interpreta una vez que sé que las dos variables tienen alta correlación.